
20 February 2024
Guess and check is a method our children are taught when they are in their early primary years. While it is reliable and guarantees the right answer if a student were to spend enough time on each calculation, a school examination does not provide them with the luxury of going through every single one of them.
Another downside of guess and check is that it involves an element of luck, as well as how strong the logical skills of your child are. If your child happens to get the answer right in their first or second calculation, then they can move on relatively quickly, but if it involves multiple tries to reach the right solution, examinations and timed tasks can turn into a difficult affair.
Continue reading below if you would like to know when and why the assumption/supposition method should be used over guess and check.
The assumption/supposition method, also known as the supposition method, involves strategically assuming values or conditions to simplify a problem. Unlike guess and check, which depend on trial and error, this method relies on logical deductions and problem-solving strategies to ease the solution process. The assumption method can be a highly efficient method compared to guess and check, especially since it provides targeted and strategic solution attempts via logical reasoning.
The assumption method is best employed when your child needs to:
Knowing when to apply the assumption method and adding helpful illustrative guides to visualise the problem at hand can make a difference in successfully solving a seemingly complicated math problem.
When these 3 key information are presented in the question:
If these information are present, the question can be solved using Supposition Method instead of Guess and Check method.
When deciding if the assumption method is ideal for solving a question, you should keep these tips in mind.
Here is an example of the assumption/supposition method in action:
John invited 30 boys and girls to his birthday party. He gave 5 chocolates to each boy and 2 chocolates to each girl. If John gave away 141 chocolates, how many girls did John invite?
Step 1
Assume all are boys (assume the opposite of what the question is asking for. Eg: Qns asking for how many girls so assume opposite = boys)
Total number of chocolates = 30 X 5 = 150
Step 2
Find the difference between the actual and assumed
Extra chocolates = 150 – 141 = 9
Step 3
Find the extra number of chocolates needed for every exchange from 1 boy to 1 girl.
1 exchange = 5 – 2 = 3
Step 4
Find the number of exchanges needed. This will give us the number of girls (when we assume all are boys in step 1, step 4 will give the opposite i.e. girls)
No. of exchanges = 9 ÷ 3 = 3 (no. of girls)
If the question is asking for both girls and boys such as: “How many boys and girls did Yenni invite?”
Step 5
Find the number of boys. Since we know that girls = 3, we can use the total number minus the number of girls
No. of boys = 30 – 3 = 27
In a test, there were a total of 40 questions. For every question answered correctly, a student was awarded 4 points. For each question answered wrongly, 1 point was deducted. If Anna scored 130 points, how many questions did she answer wrongly?
Step 1
Assume all questions answered are correct (Penalty Question, always assume the positive that adds value/earned For e.g.: this question: assume those that are correct to be awarded points).
Total no. of points = 40 X 4 = 160
Step 2
Find the extra number of points that needs to be removed to obtain the actual points.
Extra points = 160 – 130 = 30
Step 3
Find the extra number of pointsdeducted for every exchange from 1 correct question to 1 wrong question.
1 exchange = 4 + 1 = 5
(It is an “addition” for due to the fact that I not only lose the 4 points from removing 1 correct question, I also had to deduct 1 point when I change it to a wrong. As such, I lose 5 points each time I change from a correctly answered question to a wrongly answered question.)
Step 4
Find the number of exchanges needed. This will give us the number of wrong questions (when we assume all questions are correct in step 1, step 4 will give the opposite i.e. wrong questions)
No. of exchanges = 30 ÷ 5 = 6 (wrong questions)
Step 5
Find the number of correct questions. Since we know that wrong questions = 6, we can subtract the number of wrong questions from the total number of questions.
No. of correct questions = 40 – 6 = 34

With the PSLE examination only a month away, there is a palpable tension among students who are apprehensive about the questions they will receive. With time being of the essence, strengthening math foundations is essential to solving problems efficiently and with little difficulty. The assumption (or supposition) method is one of the many problem-solving tools at your child’s disposal, and it can be a highly important one to help them complete the PSLE Maths paper on time.
We have provided a few math problem sums in this article to help your child understand how to use the assumption method effectively and in different ways.
Let us try a simple question to get you going:
Mrs Lim, Mrs Chan, and Mrs Ong took part in a baking competition. They baked a total of 465 cupcakes. Mrs Lim baked three times as many cupcakes as Mrs Chan and Mrs Ong baked 30 cupcakes more than Mrs Chan. How many cupcakes did Mrs Ong bake?
The first thing to do is break down the questions into something easily understood. From the question, we know that:
Based on this, we can draw a simple graphic to visually represent the problem at hand.
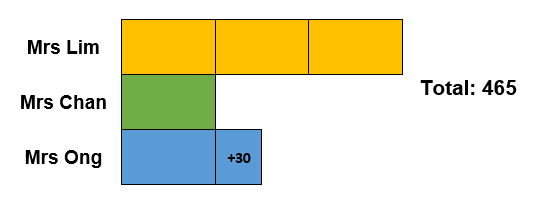
Since Mrs Lim baked three times as many cupcakes as Mrs Chan, we can work with the assumption that each block in the diagram (excluding Mrs Ong’s 30 more cupcakes) is the same amount. Thus:
465 – 30 = 435
435 ÷ 5 = 87
Add this information to your diagram if you think it helps.
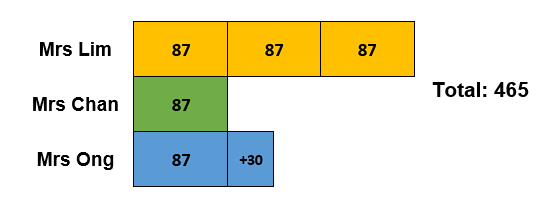
With the information in place, we can quickly see how many cupcakes Mrs Ong baked.
87 + 30 = 117
Well done! That was not too hard, was it?
Now, let us look at the next question.
A car park has a total of 30 trucks and motorcycles. If there are 102 wheels in total, how many more buses than motorcycles are there?
Why not solve this yourself and compare your answer to our solution this time? There is no harm in not getting it right the first time; practice makes perfect. Take time to formulate your solution based on what you learned in the first question. It may also be helpful to time yourself to see how fast you can come up with the solution; it could be an excellent motivator to show you are making good progress.
Ready to go?
As usual, break down the question into understandable parts first.
Put this information into a simple graphic to help you better understand the problem.

Let us start by assuming that only buses are in the car park. That would mean:
30 x 4 = 120
We now have 120 wheels since we consider every vehicle in the car park to be a bus. We know there are actually only 102 wheels in the car park. That means we are currently in excess:
120 – 102 = 18
A motorcycle has only two (2) wheels, and we currently have 18 vehicles in excess. To reduce the total number of wheels by 18, how many motorcycles do we need to replace the excess buses?
18 ÷ 2 = 9
30 – 9 = 21
Therefore, there is a total of 21 buses in the car park. That would mean the difference between the number of buses and motorcycles would be:
21 – 9 = 12
If you have spare time, you can double-check your work to ensure you arrive at the correct answer.
Onto the next question!
Mary has 60 notes in her purse, consisting of only $20 and $50 notes. If the total value of her notes is $2340, how many $50 notes does Mary have?
Once again, try this question on your own first before checking our solution.
As usual, let us break down the question.
Let us assume that Mary only has $50 notes in her purse.
$50 x 60 = $3000
Naturally, we have an excess of money in her purse. How much of a difference, exactly?
$3000 – $2340 = $660
A visual representation of this could help.

With that in mind, how do we determine the number of $20 notes Mary has? We may need a clear breakdown of the notes in her purse because we have a mix of $50 and $20 notes in her purse.
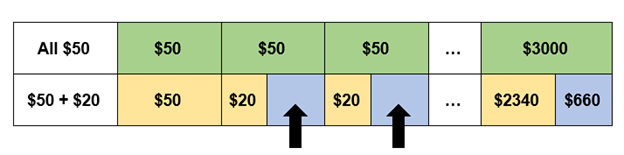
Notice how there are gaps in the distribution of notes. In the context of the question, these gaps represent the excess money that we determined earlier, that being $660. Finding the value of each gap is relatively straightforward:
$50 – $20 = $30
Since the excess is $660, we can now find the number of gaps:
$660 ÷ $30 = 22 gaps
Each gap means we changed $50 to $20. Therefore, one gap represents one $20 note. The result is that you can finally determine the number of $50 notes in Mary’s purse.
60 – 22 = 38 notes
|
|
Assumption/supposition Method |
Guess and Check |
|
Approach |
Based on making educated guesses and working backwards. |
Relies on systematic trial and error. |
|
Strategy |
Utilises logical deductions and problem-solving strategies. |
Involves trying different values systematically. |
|
Efficiency |
Tends to be more efficient, as guesses are based on logic. |
Can be time-consuming, especially for complex problems. |
|
Precision |
Allows for targeted and strategic solution attempts. |
May involve luck and exhaustive iterations. |
|
Complexity Handling |
Effective for problems with multiple variables or constraints. |
Suitable for simpler problems or situations with few variables. |
|
Time Sensitivity |
Advantageous in timed scenarios or examinations. |
May not be ideal for time-constrained situations. |

When faced with math problems that have multiple variables and require a strategic approach, the assumption/supposition method should be your go-to choice. You break down what seems like a complex problem into manageable steps and avoid being overwhelmed. From there, you are shown a clear pathway to getting closer to the solution with each step taken. This can help students who tend to panic when faced with tough questions, especially when they are racing against the clock.
If you’re working under exam conditions, the supposition method can be a lifesaver. It gives you a structured framework within which can help you stay focused by strategically narrowing down your options based on educated assumptions. This can increase your chances of finding a solution within the allotted time.
The importance of avoiding errors cannot be overstated, especially in complex problem-solving scenarios. When combined with being under exam conditions, every mistake is precious marks lost as the student risks being unable to complete the paper within the time limit. If the situation calls for the minimization of errors, the supposition method directs the student to take a systematic approach guided by logic. This reduces the possibility of overlooking important details or coming to the wrong conclusions.
Complex math problems can be overwhelming, especially if your child has a weak foundation in the subject. By making logical assumptions, the supposition method allows students to focus on specific aspects of the problem one at a time. This simplification process helps students gain a clearer understanding of the problem and makes it easier to identify potential solutions or paths forward.
The assumption/supposition method offers a structured framework for approaching math problems. Instead of feeling overwhelmed by a problem’s complexity, students can follow a step-by-step process that guides them through the problem-solving process. This structure provides clarity and direction, helping students stay focused as they work towards finding a solution.
It is common for students to feel nervous when faced with exams. However, if it heightens at the sight of a math problem they find complicated, their mind may go blank, which can affect their performance. By breaking down the problem into manageable steps through the supposition method, students can build confidence as they make steady progress towards finding a solution.
The assumption/supposition method is about more than finding the right answer. It is about teaching students how to think critically. They’re encouraged to consider different perspectives, weigh evidence, and draw logical conclusions. This not only helps them solve math problems more effectively but also equips them with crucial skills for navigating real-world challenges.

Click HERE to attend a free 38-minute online course.
Course Highlights:

The assumption method can be a lifesaver in helping students tackle complex questions that can be confusing at first. Still, those with a weak foundation in maths may need continuous practice and support before they can start employing it in their problem-solving strategies. At Matrix Math, we provide primary math tuition designed to empower and nurture independent learners to effectively use the assumption method in solving mathematical problems.
Contact us today to sign your child up for our comprehensive math lessons and help them excel in the subject!