25 November 2025
Number patterns are an integral part of our lives. As students strengthen their mathematical foundations, their pattern recognition abilities will help them understand how number sequences can form. From simple linear number series to the complex Fibonacci sequence, number patterns play a key role in solidifying a student’s mathematical foundations, especially when tackling more advanced concepts, such as geometry and probability.
Consider the following number sequence:
1 5 9 13 17 21
Each number in this sequence is a term, with the first term (T1) being the number 1, and the fifth term (T5) being the number 17. This sequence follows a pattern in which students add 4 to the current term to obtain the next one. For example, the second term (T2) 5 is derived by adding 4 to the first term (T1).
The general term of this linear number sequence is represented as Tn. To find a specific term in this sequence, as well as other similar sequences, students may use this formula:
Tn = a + (n – 1)d
In this formula, “n” represents the ordinal numerical value of a term in the sequence, while “a” corresponds to the first term of the sequence, and “d” is the common difference between two terms. Students can use this formula to find any term in a sequence without tediously listing all previous terms.
Using the earlier example, if we want to find the 100th term in the sequence:
1 5 9 13 17 21…
n = 100, a = 1, d = 5 – 1= 4
T100 = 1 + (100 – 1)(4) = 1 +(99)(4) = 397
Number pattern formulae may have different rules depending on the type of sequence. Pay close attention to how the sequence progresses and the difference between consecutive terms to help determine the appropriate rule to use.
Simply put, a square number sequence is made up of a series of numbers that are each multiplied by themselves. The following sequence is a series of square numbers:
1, 4, 9, 16, 25…
12, 22, 32, 42, 52…
The formula for square numbers is straightforward:
Tn = n2
Pattern recognition is a key concept that helps students identify the formula for the number pattern they encounter. Obtaining the right formula starts with these steps:
First, carefully study the number sequence provided and determine the underlying pattern as students move from one term to the next. Consider this example sequence:
2, 7, 12, 17, 22…
In this case, each term increases by a constant amount of five.
Various types of sequences follow different patterns that determine their terms. Students should always double-check that the sequence matches the identified number pattern. In our previous example, it is an arithmetic sequence because it increases by a constant of 5.
2 (+5) 7 (+5) 12 (+5) 17 (+5) 22 (+5) …
Students will need to use a combination of arithmetic operations, powers of numbers, and algebra to correctly apply the formula. They can then generalise the number pattern and apply it to every term in the sequence, including terms not provided.
Using the above example, the first term (T1) is two. We then progressively add the constant 5 to each term to find the subsequent terms. If we wish to determine the nth term (Tn), we will use two in the formula and add (n – 1) multiplied by the common difference between any two consecutive terms.
Tn = 2 + (n – 1)5
Tn = 5n – 3
Now that the formula is set, verify your answer by checking whether it correctly predicts the terms in the sequence. For example, by using the second term (T2):
T2= 2 + (2 – 1)5 = 2 + 5 = 7
It is always good practice to triple-check the formula to ensure students get the correct answer.
Consider the following figures of circles and squares.
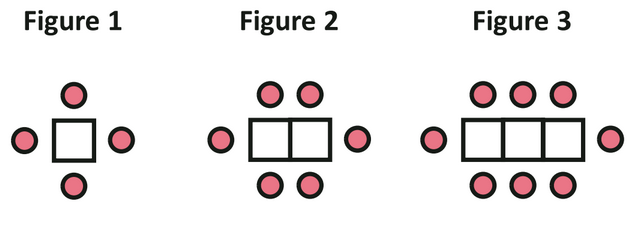
It helps to illustrate the sequence using a table.
Figure | No. of circles | No. of squares |
1 | 4 | 1 |
| 2 | 6 | 2 |
| 3 | 8 | 3 |
Note that the number of circles increases by 2 for each subsequent figure, while the number of squares increases by 1.
If you need to determine which figure has 38 circles, you can start by subtracting 4 from 38, as the first figure begins with 4 circles:
38 – 4 = 34
As the number of circles increases by 2 for each subsequent figure, you will then divide 34 by 2 to determine the number of intervals to reach the figure with 38 circles:
34 ÷ 2 = 17
To find the figure, add 1 to the above sum to account for starting from the first figure.
17 + 1 = Figure 18
If you are asked to find the number of circles in Figure 100, you can start by determining how many squares there are in Figure 100. Doing so is relatively straightforward, as the table shows that the number of squares corresponds to the figure number. As such, Figure 1 has 1 square, Figure 2 has 2 squares, and so forth.
Figure 200 = 200 squares
Number of intervals to Fig. 200 = 200 – 1 = 199
From there, you can work your way backwards from Section A’s methodology.
199 × 2 = 398
398 + 4 = 402
Thus, there are 402 circles in Figure 200.
Consider the following rows of circles:
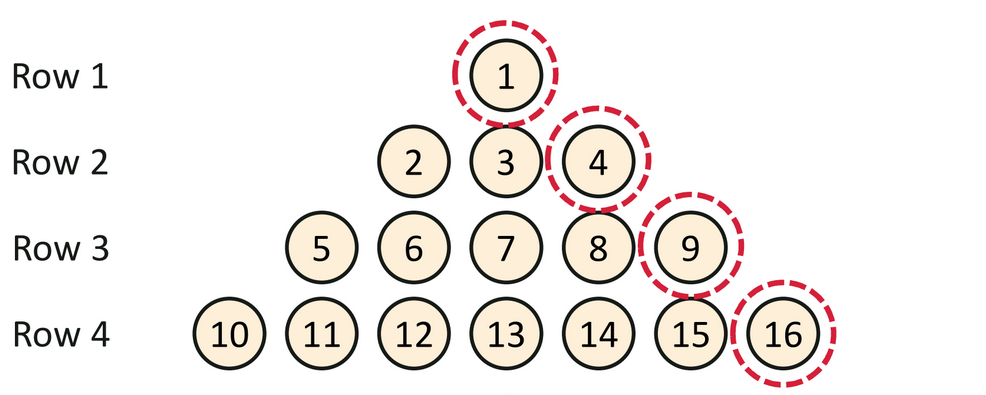
Note the number sequence highlighted by the red circles. It progresses to 1, then 4, and subsequently 9 and 16. This sequence would form a square number pattern.
1, 4, 9, 16
12, 22, 32, 42
You will notice that the largest number for each row coincides with the base value of the square. For example, row four’s highest number is 16, which is obtained by multiplying 4 (the base value) by itself.
If you need to find the highest number in row 16, you can therefore multiply 16 by itself, as follows:
Row 16 = 16 × 16 = 162 =256
If you need to determine how many numbers there are in row 16, you can subtract row 16’s highest number from row 15’s largest number:
Row 16 = 16 × 16 = 162 =256
Row 15 = 15 × 15 = 152 =225
Numbers in row 16 = 256 – 225 = 31
At Matrix Math, we guide students to success through personalised tutoring to help them understand number patterns and apply the correct formulae. We use valuable revision materials to strengthen their understanding further and build a strong mathematical foundation. Contact us today to learn how we can help your child succeed.