Matrix Math logo
heuristic math

Mastering Problem-Solving with Heuristic Maths in Singapore

09 January 2026

BY: matrixmath

Problem-solving in Mathematics gradually becomes increasingly complex as students develop their mathematical foundations. Heuristics provide students with invaluable tools for better understanding a maths problem and solving it effectively.

What is Heuristic Maths?

Heuristic maths is built on the notion of “heuristics”, strategies or mental shortcuts that help students understand and solve different types of maths problems. Think of them as a rule of thumb for systematically solving a given maths problem, reducing the time and effort needed to find the answer.

It is essential to note that heuristics do not guarantee a solution, nor do they provide specific steps to achieve one. Instead, heuristics guide students in making judgments about how to approach a problem, usually by breaking it down into more manageable parts, helping them to reach the correct answer.

The Curriculum Planning and Development Division (CPDD) of the Singaporean Ministry of Education (MoE) has prepared a comprehensive framework that covers several heuristics applicable to primary Mathematics lessons. These include (but are not limited to):

  • Act it out
  • Use a diagram or model
  • Use guess-and-check
  • Look for patterns
  • Work backwards
  • Make a systematic list

Why Heuristic Maths Matters

Solidify Maths Foundations

Learning Mathematics should not rely on rote memorisation, as it does not promote conceptual understanding of maths concepts. Heuristics aims to facilitate a gradual knowledge of mathematical concepts, which then helps students understand how to apply the concepts and formulae they have learned correctly. This further enhances their mathematical foundations and prepares them for future learning.

Simplify Problem-Solving

With a strong mathematical foundation, students can almost immediately tell which concepts, formulae, and heuristics can help them solve a given problem. This allows students to spend less time searching for a solution, as they know what to do based on the available information. Learning Mathematics should not rely on rote memorisation, as it does not promote conceptual understanding of maths concepts. Heuristics aims to facilitate a gradual knowledge of mathematical concepts, which then helps students understand how to apply the concepts and formulae they have learned correctly. This further enhances their mathematical foundations and prepares them for future learning.

Raises Confidence

Heuristics also help build students’ confidence as they become more comfortable in solving unfamiliar or complex maths questions. This prepares them for more advanced lessons as their skills develop, and their maths anxiety wanes with time and experience.

Transferable Skills

Heuristic maths also teaches students how to apply their maths lessons to real-world situations. It equips them with transferable skills that they can rely on in the future, whether to complete daily tasks or even support their career development.

Common Types of Heuristic Maths Taught in Singapore

Act It Out

Learning Mathematics should not rely on rote memorisation, as it does not promote conceptual understanding of maths concepts. Heuristics aims to facilitate a gradual knowledge of mathematical concepts, which then helps students understand how to apply the concepts and formulae they have learned correctly. This further enhances their mathematical foundations and prepares them for future learning.

Look for Patterns

Students will learn how to spot repeating structures or trends, and can then make predictions based on this information.

Consider the following number sequence:

1 2 3 5 9 1 2 3 5 9 1 2…

Students will be able to identify a repeating pattern consisting of five numbers.

1 2 3 5 9

If they are asked to find the 15th number in the sequence, their answer will be 9. This is because the number 9 is the 5th number in the repeating pattern.

Draw a Diagram/Model

Students can also use a handy diagram or model (such as a table) to illustrate the maths problem and its variables. To illustrate, consider the following graphic:

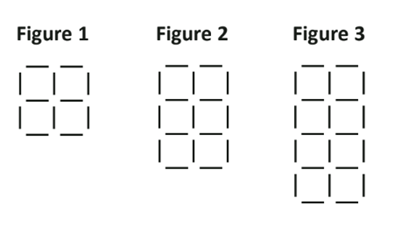
diagram

Students are asked to find the number of squares in Figure 10. They should first prepare a diagram to help visualise the changes from figure to figure:

Figure 14Baseline
Figure 26+2
Figure 38+2
Figure 410+2
Figure 512+2

From there, they can gradually solve the equation.

No.of intervals: 10 – 1 = 9
1 interval adds 2 squares
9 intervals from Figure 1: 9 × 2 = 18
No.of squares in Fig.10: 18 + 4 = 22

Restate the Problem Differently

Students can rewrite or rephrase the question to make it easier to understand. For example, students are asked to determine how many toy blocks A currently has left if A lent three-quarters of their 20 toy blocks to B.

Fractions can be confusing, so restating them may be beneficial. In this case, A has one-quarter of their blocks left. The question now becomes, “What is one-quarter of 20 blocks?”

4 quarters: 20 blocks
1 quarter: 20 ÷ 4 = 5 blocks

Thus, A now has five blocks left.

How Heuristic Maths is Taught in Schools and Tuition Centres

Heuristic maths is taught using George Polya’s Four-Step Problem-Solving Process as the guiding framework. It primarily focuses on four key steps:

Understanding the Problem

Students must be able to determine what the question expects from them based on the information provided. To facilitate this, teachers and tutors should facilitate student understanding by asking guiding questions related to the problem:

  • What do you need to find?
  • What parts are irrelevant?
  • What model can you use to illustrate the problem?
  • Do you have sufficient information to solve this?

 

Heuristics cannot be explicitly taught, as they can limit their applicability across a wide range of mathematical scenarios. Therefore, teachers and tutors can guide students through the process and help them gradually figure things out independently with enough practice.

Making a Plan

Once students have a complete understanding of the maths question, they can devise a suitable strategy by picking appropriate heuristics to help solve the problem. Teachers and tutors should guide students in formulating an understanding of how to apply a heuristic to reach the desired solution, such as using a diagram to identify patterns.

Executing the Plan

Students can then systematically apply their problem-solving strategy to find the answer. If the strategy does not work, students must be able to improvise using a different heuristic approach.

Look Back and Review

Students should then recheck their answers and confirm that their chosen heuristic approach has helped them find the correct answer. Teachers and tutors should encourage self-checking and classroom discussions to further build students’ foundations, enabling them to gain a firmer grasp of the subject and answer maths questions confidently.

Want to learn more about how we apply Polya’s framework to our Primary Maths tuition classes? Contact Matrix Math today to find out more about our approach to heuristic maths!

Read Also:

  • Unlocking Success: The Crucial Role of Primary Maths Tuition In Excelling At PSLE Maths

  • How to Help Your Child Develop Early Math Skills

  • Understanding The Changes of Primary 5 Maths Syllabus

  • Is The PSLE Paper Really That Tough?

  • Guess & Check Math Questions Solutions

    • BACK TO BLOG